Assume v. Presume

[gomezz]

Huh? Not true for the set of integers which is a subset of the set of reals:

 

[Black Hole]

Those are different infinities. How did we divert from language pedantry to maths?

 

[prpr]

42.
Oh, er, no, that's not the right answer. Or perhaps it wasn't the right question.

 

[EEPhil]

Found this on the BBC News text pages (and also online http://www.bbc.co.uk/news/science-environment-31483629)

Scientists are tracking snails from space in a bid to combat the spread of parasitic disease in Africa.

Am I missing something? Snails from space? When did we determine there was extraterrestrial life?
I wonder if they mean - Snails are being tracked from space by scientists in a bid...

 

[prpr]

I wonder if they mean - Snails are being tracked from space by scientists in a bid...

Or just put in some punctuation to make it clear...
Snails are being tracked, from space, by scientists in a bid...

 

[Black Hole]

Nah, that would be "Scientists are tracking snails, space, a bid to combat..."

 

[EEPhil]

Or just put in some punctuation to make it clear...
Snails are being tracked, from space, by scientists in a bid...

Isn't this rewriting my attempt at correcting the BBC's mistake?
I am only a failed engineer not a pedantic linguist, so I may be wrong, but I'm beginning to doubt my own attempt. It still looks to me as though the snails are arriving from space. How about - Scientists are using satellites to track African snails in a bid to combat the spread of a parasic disease.

 

[Black Hole]

It still looks to me as though the snails are arriving from space.

No, you were OK with that (plus some punctuation).

 

[prpr]

Isn't this rewriting my attempt at correcting the BBC's mistake?

Possibly. I can't remember what I was thinking about now.
Anyway, having read the article, the opener is a complete lie. There are no snails from space, and there is no tracking of snails (from space or anywhere else).
They are just use satellites to make maps as far as I can tell. This is NOT tracking. He then witters on further down the page about how his own statement is false. It's crap journalism.

 

[EEPhil]

No, you were OK with that (plus some punctuation).

What punctuation, in your opinion (or, in fact ), did I miss?

 

[Deleted member 473]

Huh? Not true for the set of integers which is a subset of the set of reals:

Both the integers and the reals are infinite, and both are in 1-1 correspondence with a subset of themselves. No contradiction!

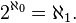
For the integers, Z, let N be the (strict) subset of natural numbers {1,2,3,...} and define f:N->Z by

f(n) = n/2 if n is even
f(n) = - (n-1)/2 if n is odd

I leave the real case as a simple exercise.

 

[EEPhil]

Not really an assume v presume topic. According to another BBC News item "Black hole's blast stunts birth of stars" http://www.bbc.co.uk/news/science-environment-31556326.
"Winds blasted out by the giant black holes..." What have you been eating?

 

[Black Hole]

You get out what you put in.

 

[gomezz]

Both the integers and the reals are infinite, and both are in 1-1 correspondence with a subset of themselves.

But the set of integers is a subset of the set of reals but is *not* in a one to one correspondence.

Perhaps what you meant to say that there exists a strict subset which is in one to one correspondence? They way you phrased it could be read as meaning *any* subset is in one to one correspondence. A good example of how sloppy language can be used to slip through an unnoticed and unquestioned invalid assumption which breaks the chain of logic.

 

[kevindickinson]

What happens if you want a bag of nuts to go with your drink?


Sent from here using a computing device.

 

[EEPhil]

What happens if you want a bag of nuts to go with your drink?

1) In a bar: Ask the bar staff nicely and they might sell you a bag.*
2) In a hardware shop (eg. Wilkinsons) : Find the nails, screws and bolts section and you might find a bag of nuts. Then go to the food end of the shop and pick up your drink.
3) In America: Make sure you asked for your drink to go as well. Otherwise the nuts may leave whilst you're still drinking.
4) If you tie up some people with mental illnesses in a bag and tell them to leave with your drink - you should be locked up!
* Be careful or you might find the bag of nuts IN your drink. (I once asked for a Brown & Mild, and a Coke at a bar and the barman wanted to put them in one glass. I think he was joking.)

 

[Deleted member 473]

Perhaps what you meant to say that there exists a strict subset which is in one to one correspondence? They way you phrased it could be read as meaning *any* subset is in one to one correspondence. A good example of how sloppy language can be used

My sloppy language is better than your sloppy language!

Any mathematician would have interpreted what I said correctly. I never said "any strict subset."

 

[Deleted member 473]

Giving peace of mind a piece of your mind? Top review:

http://www.amazon.co.uk/ETHERNET-NETWORK-CAT5E-CABLE-TESTER/dp/B007CJUEDA/#customerReviews

At least he didn't say "it does what it says on the tin", though, unlike G O Purvis further down.

^ Note the ", instead of the totally illogical, but accepted, ," above.

 

[gomezz]

Any mathematician would have interpreted what I said correctly

If I had had my mathematician's hat on I would not have attempted to interpret what you said.

 

[Deleted member 473]

If I had had my mathematician's hat on I would not have attempted to interpret what you said.

It's informal mathematics, what mathematicians talk, rather than write in research papers. With your interpretation, the only infinite sets would have to be in 1-1 correspondence with their empty subset, meaning all infinite sets would be empty!